homebusinessblogart

Partnerships and Coalitions

Core games

The core game:

Empty core game:
v(AB) = 118
v(BC) = 50
v(AC) = 84
v(ABC) = 121

Core

Core:
Alternative definition: Set of allocations against which you cannot make an objection

Objection: Let $x$ be a proposed allocation. Let $k \neq l$ be two players in the coalition.

Objection of $k$ against $l$ is a pair $(C,y)$:
Counter objection: $x$ is the originally proposed allocation, $k$ objects to $l$ -- $(C,y)$'s counter objection $l$ to $k$ is a pair $(D,z)$
Justified objection: An objection that has no counter objection
Bargaining set: That allocation that has no justified objection.

Nucleolus: Most fair allocation among the stable allocations. Nucleolus exists in the bargaining set. If core is not empty, nucleolus will be at the center of the core.

Exercise 1


Find an unjustified objection to the allocation with counter objection: (79,39,3). Also,find a justified objection.

v(AB) = 118
v(BC) = 50
v(AC) = 84
v(ABC) = 121

Nucleolus solution: $(74\frac{1}{3},40\frac{1}{3},6\frac{1}{3})$ there will always be a counter objection.

Core is allocations with no objection. Core can be unfair

Exercise 2: Glove game

A Left
B Right
C Right

v(A) = 0
v(B) = 0
v(C) = 0
v(AB) = 1
V(BC) = 0
V(AC) = 1
v(ABC) = 1

Q. Is the allocation in core: (1,0,0) : Yes
Q. Is this a core allocation: (0,1,0) : No

(1,0,0) is the only stable solution -- core is non empty

Q. Where is nucleolus? Nucleolus is inside core. Core has one solution. This allocation (1,0,0) is the nucleolus.

Q. Is (1,0,0) fair? Nope. Competition in B and C is leading to A to squeeze out from them. Prisoners Dilemma/ Gaming nature between B and C is hurting both of them.

Least Core


Core: $x(s) \leq c(s)$

Least core:
unhappiness = $u(x) = x(s) - c(s)$
$u(s) <= e$ ; minimize $e$

Calculating Nucleolus

For a general problem, nucleolus is calculated by iteratively decreasing unhappines after finding least core allocation.

Shapley Value

(1) All value should be allocated $$\sum_i x_i = v(N)$$
(2) Symmetry: For all $s \subseteq N\\{i,j}$, where $$v(s \cup {i})-v(s) = v(s \cup {j})-v(s)$$ Then, $$x_i = x_j$$
(3) Dummy player property Suppose $$v(s \cup {i}) = v(s) + d \ \forall S \subseteq N\\{i}$$ Then $$x_i = d$$
(4) $w(s) = k \times v(s) \forall s \Rightarrow$ the allocation in $x_i^w = kx_i^v$



Calculating shapely value:

Average of the marginal value player $i$ brings in permutations of players that have been chosen before $i$

$$\text{Shapely Value} = \sum_{S \subseteq N\\{i}} \dfrac{|S|!(n-|S|-1)!}{n!}\left(v(S\cup{i})-v(s)\right)$$

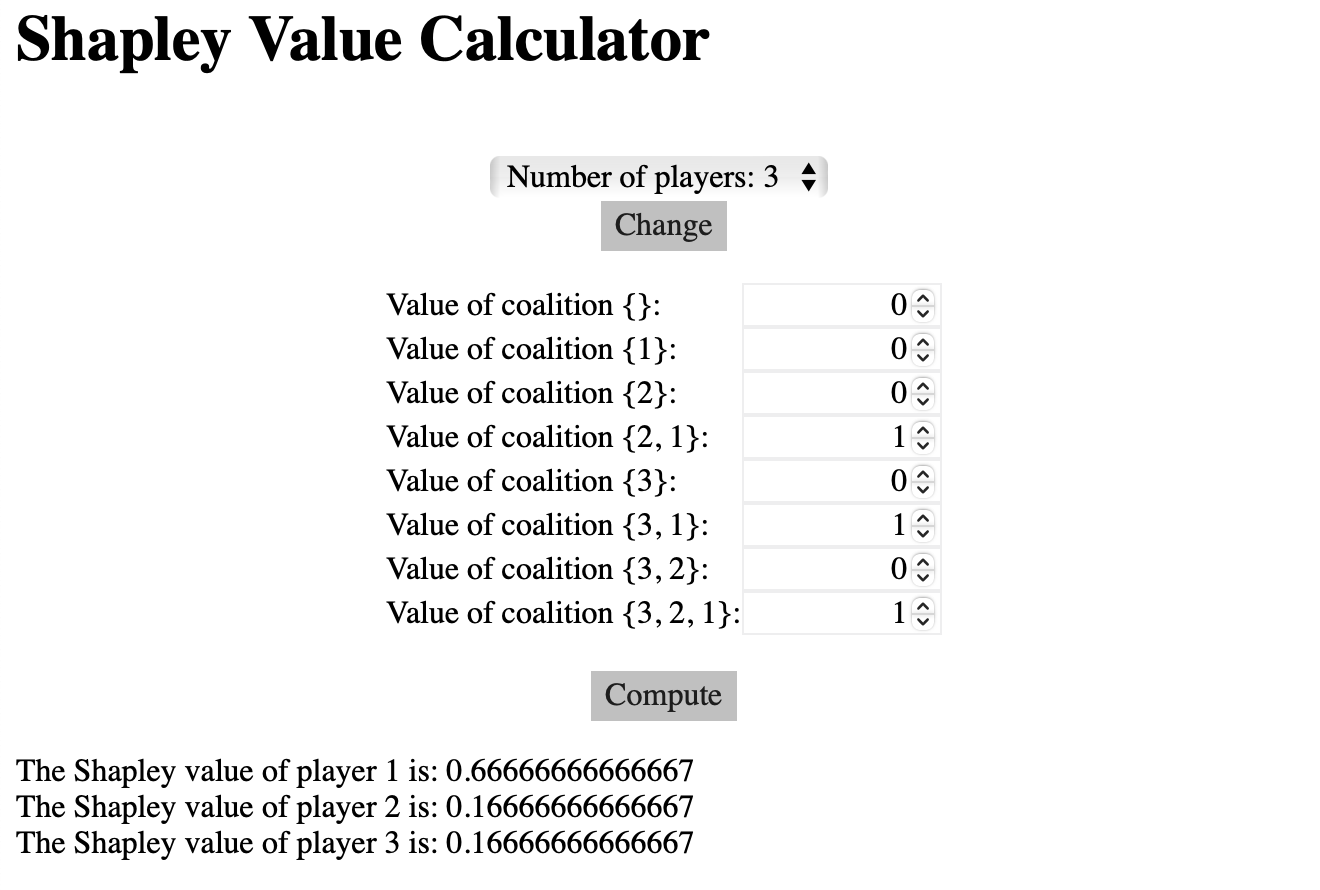
Exercise 3

Calculate shapely value for glove game:
(1) Hard way -- solve it yourself
(2) Easy way -- shapelyvalue.com

Shapley Value For Glove Game

Voting Ideas

How to take group decisions?

Top preference: Voting just the "top choice" is not ideal, votes could divert the existing majority votes to newer/other choices.

Assigning value to each rank (Weighted allocation): Susceptible to change to an irrelevant non-winning choice can impact the winning choice.

Multiple two-way elections A>B, B>C, C>A --> ???

Elimination voting: Collecting all preferences for voting, eliminate who score least for 1st rank and so on. Issue: Person with massive victory could lose if a few people change their votes to prefer the winning person.



Kenneth Arrow-- Any voting protocol between 3 or more alternatives will have one of these flaws:
1. Invalid (No results/)
2. Tactical voting
3. Disctatorship (One person's vote decides everything)



(1) Never decide things by voting A>B, B>C, C>A
(2)Try debate and convince (consensus)

Exercise 4: UN Security Council


Scenario 1 (Older): Permanent Members |P| = 5, Non-permanent |T| = 6
$$v(S) = 1 if P \subseteq S \suchthat |S| \geq 7, 0\ \text{otherwise}$$

Scenario 2 (Newer): Permanent Members |P| = 5, Non-permanent |T| = 10
$$v(S) = 1 if P \subseteq S, |S| \geq 9, 0\ \text{otherwise}$$

Calculating power of countries using shapely value:

[Scenario 1] All 5 Permanent member + 1 Non Permanent member before you. $$\text{Shapley value of single non permanent member} = 1 \times 5 \times \dfrac{6! \times 4!}{11!} = 0.002$$ Now, calculating power of one permanent member: $$6t + 5p = 1 \Rightarrow p = 0.19$$ Hence, permanent members have 90x power than non permanent members.


[Scenario 2] All 5 Permanent member + 3 Non Permanent member before you. $$\text{Shapley value of single non permanent member} = 1 \times ^9C_3 \times \dfrac{8! \times 6!}{15!} = 0.001865$$ Now, calculating power of one permanent member: $$10t + 5p = 1 \Rightarrow p = 0.19$$ Hence, permanent members have 105x power than non permanent members.

Elevator game

1. Apartment building with 6 floor, 4 houses per floor
2. 72000 Euros for building a lift
3. Heterogenous factors: (1) Lower floor people might not need it (2)

Absense of value creating strategies. People could overstate/ understate the value. Home Owner's Association could enforce rules.

Q. When do we want the lift?

$v_i$ : Private valuation of the home owners

Construct if $\sum v_i \geq V = 72000$

Q. How to not incentivize lying Eliminating conflict of interest. Example: "How much did others work in the group assignment?" This eliminates the consequences of your answer and what is reported for others.

Pivot mechanism


Pivotal person Single person whose single high/low valuation changes the entire group's. They are to be penalized for the huge gap between the fair value and their bid.